Karşılıklı Etkileşim Diyagramı Hazırlanması
Dikdötgen kesitli bir betonarme elemanın, TS-500’e göre karşılıklı etkileşim diyagramı, kontrol noktalarındaki gerilmelerin hesaplanmasıyla kolayca hazırlanabilir. Dikdörtgen bir kesit için birim şekil değiştirme ve gerilmeler $\varepsilon_{cu}=0.003$ için Şekil-1’de gösterilmiştir.
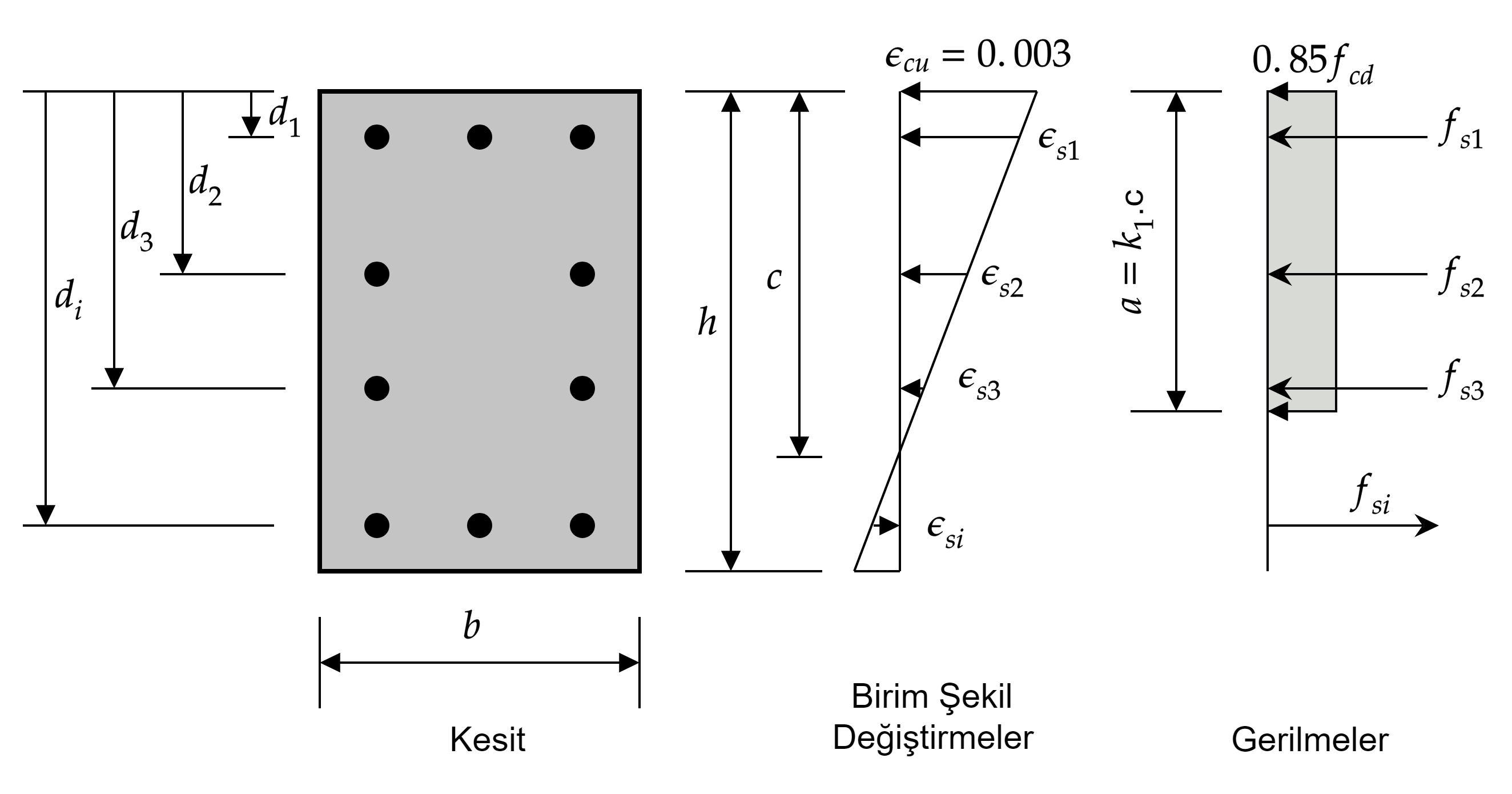
Benzer üçgenlerin eşitliğinden donatı çubuğundaki uzama $\varepsilon_{si}$, $c$ tarafsız eksen derinliği ve $d_{i}$ donatı çubuğunun beton üst yüzeyine uzaklığı olmak üzere Eşitlik-1 ile hesaplanır. Eşitlikten anlaşılabileceği gibi $d_{i} > c$ için $\varepsilon_{si}$ değeri negatiftir.
\(\varepsilon_{si} = \dfrac{c-d_{i}}{c}\cdot \varepsilon_{cu} \tag{1}\) Donatı çubuğundaki gerilme ise donatının akıp akmamasına göre farklılık gösterir.
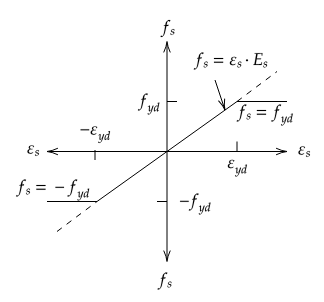
\(\begin{eqnarray} \begin{cases} \varepsilon_{si} \ge \varepsilon_{yd} \Rightarrow f_{si}=f_{yd} \\ \varepsilon_{si} \leq -\varepsilon_{yd} \Rightarrow f_{si}=-f_{yd}\\ \text{aksi halde} \; f_{si} =\varepsilon_{si} \cdot E_{s} \end{cases} \end{eqnarray} \tag{2}\) $-f_{yd} \leq f_{si} \leq f_{yd}$ sınırı dışındaki gerilmeler için donatı akmıştır.
Betondaki gerilmeler eşdeğer dikdörtgen gerilme bloğuyla ifade edilir. Beton basınç bloğu yükseklik faktörü $k_{1}$, TS-500 için Eşitlik-3’de verilmiştir. Ancak $k_1$ 0.64 değerinden küçük olamaz. \(k_{1} = \begin{eqnarray} \begin{cases} f_{cd} \leq 25 \text{ MPa} \Rightarrow 0.85 \\ f_{cd} >25 \text{ MPa}\Rightarrow 0.85 - 0.006 \times(f_{cd} -25)\\ \end{cases} \end{eqnarray} \tag{3}\) $a=k_{1} \cdot c$ için betondaki kuvvet Eşitlik-4 ile bulunur. ($a$ basınç bloğu, $c$ ise tarafsız eksen derinliği) \(F_{c} = 0.85\times f_{cd} \times a \times b \tag{4}\) Betondaki kuvveti hesaplarken beton alanı içinde donatı çubuğu alanları da bulunmaktadır. Bu nedenle donatı çubuklarındaki kuvvetleri hesaplarken $0.85 \times f_{cd}$ değerinin gerilmelerden düşülmesi gereklidir.
Böylelikle donatı çubuğundaki kuvvetler Eşitlik-5 ile hesaplanır. \(F_{si} = \begin{eqnarray} \begin{cases} d_{i} < a \Rightarrow F_{si}=(f_{si}-0.85f{cd})\times A_{si} \\ d_{i} > a \Rightarrow F_{si}=f_{si}\times A_{si}\\ \end{cases} \end{eqnarray} \tag{5}\) $F_{si}$ değeri, donatı basınç bölgesindeyse pozitif, çekme bölgesindeyse de negatiftir.
Eksenel taşıma kapasitesi $P_{n}$, kabul edilen gerilme dağılımı için Eşitlik-6 ile hesaplanır. \(P_{n}=F_{c}+\sum_{i=1}^n F_{si} \tag{6}\) Moment kapasitesi $M_{n}$ ise Eşitlik-7 ile bulunabilir. \(M_{n}=F_{c}\left(\dfrac{h}{2}-\dfrac{a}{2}\right)+\sum_{i=1}^n F_{si}\left(\dfrac{h}{2}-d_{i}\right) \tag{7}\) Simetrik olmayan kesitler içinse $h/2$ yerine, basınç yüzeyinin ağırlık merkezine uzaklığı olan uzaklığı $\overline{y_t}$ değeri konularak moment kapasitesi hesaplanabilir.

Yorum yapın