Esen Yalım Karaduman

C#, Python programlama dilleri ile uğraşan ve AutoCAD eklenti tasarımına meraklı bir mühendisim.

Kapak altından geçen akım, kuyruk suyu derinliğine $(h_2$) bağlı olarak serbest ve batmış akım olmak üzere ikiye ayrılabilir. Şekil-1’deki akım serbest, Şekil-2’deki akım ise batmıştır.

Kapak altı akımın hesabı için öncelikle akımın tipi belirlenmelidir.

Şekil-1

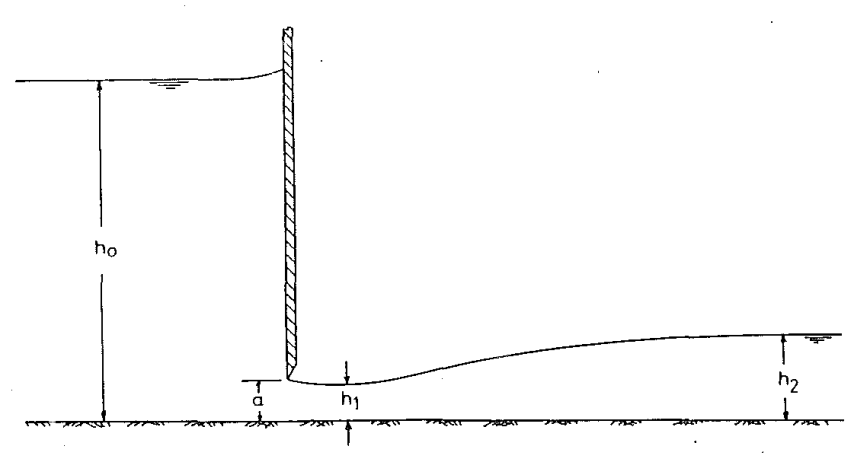
Serbest Akım Durumu

Serbest akım için debi katsayısı, $ \theta=90^\circ$ için $C_c$ büzülme katsayısı, $ a $ kapak yüksekliği ve $ h_o$ memba su derinliği olmak üzere eşitlik (1) ile hesaplanabilir.

\[C{q}=\frac{C_c}{\sqrt{1+C{c}\cdot \cfrac{a}{h_o}}}\tag{1}\]

Büzülme katsayısı $C_c $’nin hesabı için $\cfrac{a}{h_0} $ değerlerine bağlı olarak hazırlanmış aşağıdaki tablo kullanılabilir. (Werner, 1963)

\(\cfrac {a}{h_o}\) \(C_c\) \(\cfrac {a}{h_o}\) \(C_c\) \(\cfrac {a}{h_o}\) \(C_c\) \(\cfrac {a}{h_o}\) \(C_c\)
0.00 0.611 0.30 0.625 0.55 0.650 0.80 0.720
0.15 0.615 0.35 0.628 0.60 0.660 0.85 0.745
0.20 0.618 0.40 0.630 0.65 0.675 0.90 0.780
0.20 0.620 0.45 0.638 0.70 0.690 0.95 0.835
0.25 0.622 0.50 0.645 0.75 0.705 1.00 1.000

Debi katsayısı bulunduktan sonra (2) numaralı eşitlikle serbest akımın kapisitesi belirlenir.

\[Q=C{q}\cdot a\cdot B \cdot \sqrt{2 \cdot g\cdot h_o}\tag{2}\]

Batmış Akım Durumu

Şekil-1

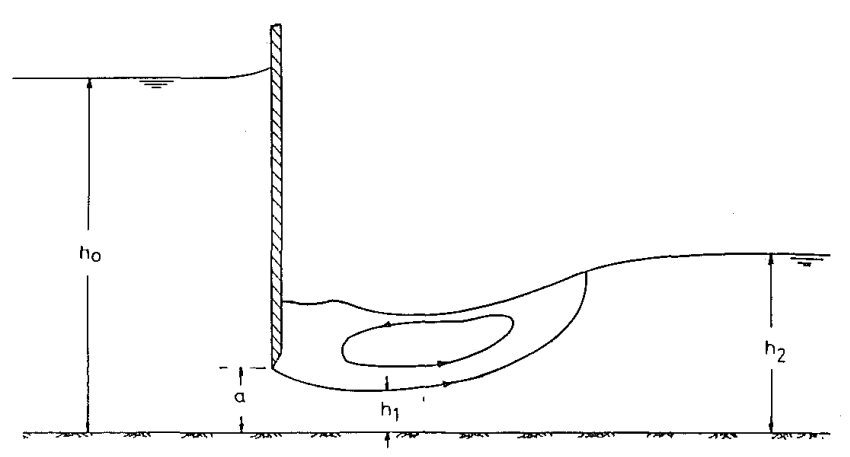
Batmış akım debi katsayısını belirlemekte kullanılan yaklaşımlardan biri serbest debi katsayısının $(\kappa$) düzeltme katsayısı ile çarpılarak batmış debi katsayısına dönüştürülmesidir. $(C^{*}_{q}=\kappa \cdot C_q $)

Düzeltilmiş debi katsayısı $C_q^*$ bulunduktan sonra (3) eşitliği ile batmış akım durumu için kapasite belirlenebilir. \(Q=C^{*}_{q}\cdot a\cdot B \cdot \sqrt{2 \cdot g\cdot h_o}\tag{3}\)

$\kappa$ düzeltme katsayısı ise (4) ve (5) eşitlikleri yardımıyla bulunabilir.

\[m = 1-\frac{2\cdot C_c \cdot \cfrac{a}{h_o}}{1+C_c \cdot \cfrac{a}{h_o}}+\frac{2\cdot C_c^2 \cdot \cfrac{a}{h_o}}{1+C_c \cdot \cfrac{a}{h_o}}\cdot \cfrac{a}{h_2}\tag{4}\] \[\kappa=\sqrt{m-\sqrt{m^2+\cfrac{h_2^2}{h_o^2}-1}}\tag{5}\]

Serbest ve Batmış Akım Sınırı

Serbest akımın sınır durumunu tanımlayan hidrolik sıçrama daralma kesitinden hemen sonra oluşur. Sıçramadan sonraki eşlenik derinlik olan $h_{2k}$’nın kuyruk suyu derinliği $h_2$’ye eşit olduğu durum için yazılan (6) eşitliğiyle sınır $h_2^*$ değeri bulunabilir.

\[A_1\cdot \overline{h_1}+\cfrac{Q^2}{g\cdot A_1}=A_2\cdot \overline{h_2}+\cfrac{Q^2}{g\cdot A_2}\tag{6}\]

$h_1=C_c\cdot a$ ve $h_{1k}=h1$ olmak üzere sınır kuyruk suyu derinliği, $h_{2}^{\ast}$ eşitlik (7) ile hesaplanabilir.

\[\cfrac{h_2^*}{a}=\cfrac{C_c}{2}\left( \sqrt{1+\cfrac{16 \cdot \cfrac{h_o^2}{a^2}}{C_c\cdot \left(C_c+\cfrac{h_o}{a}\right)}-1}\right)\tag{7}\]

Python Sınıfı

Düz kapaklar altındaki akımların serbest ve batmış durumları için

  • Debiyi, $q$
  • Memba su yüksekliğini, $h_o$

aşağıdaki SluiceGate sınıfı ile hesaplayabilirsiniz. SluiceGate sınıfı bu değerleri çözmek için scipy.optimize kütüphanesinden fsolve(...) yordamını kullanıyor.

from enum import Enum
from math import sqrt, pow

import numpy as np
from scipy.constants import g
from scipy.optimize import fsolve

class SluiceGateFlowTypes(Enum):
    FreeFlow = 1
    SubmergedFlow = 2

class SluiceGate:
    """
    Sluice-gate object
    Attributes
    ----------
    a : float
        Gate opening (m)
    b : float
        Gate width (m)
    q : float
        Discharge (m3/s)
    ho : float
        Upstream depth (m)
    h1 : float
        Depth at vena contracta (m)
    h2 : float
        Downstream depth (m)
    hcr : float
        Critical depth (m)
    h1k : float
        Upstream conjugate depth (m)
    h2k : float
        Downstream conjugate depth (m)
    Cc : float
        Contradiction coefficient
    Cq : float
        Discharge coefficient
    flowType : SluiceGateFlowTypes
        Flow type (free or submerged)
    """

    def __init__(self, a, b, q=0.0, ho=0.0, h2=0.0):
        self.a = a
        self.b = b
        self.q = q
        self.ho = ho
        self.h2 = h2
        self.h1 = 0.0
        self.h1k = 0.0
        self.Cc = 0.0
        self.Cq = 0.0
        self.hcr = 0.0
        self.flowType = None
        if q == 0.0:
            self.solve_discharge()
        else:
            if h2 == 0.0:
                self.free_flow_ho()
            else:
                self.submerged_flow_ho()
        self.hcr = critical_depth(self.q, self.b)
        v1 = self.q / (self.h1k * self.b)
        fr1 = v1 / sqrt(g * self.h1k)
        self.h2k = self.h1k * (sqrt(8 * pow(fr1, 2.0) + 1.0) - 1.0) / 2.0

    def solve_discharge(self):
        """ Solves discharge with the given values of a, b, ho and h2
        """
        self.Cc = free_flow_contradiction_coefficient(self.a, self.ho)
        self.h1 = self.Cc * self.a
        self.h1k = self.h1
        self.flowType = flow_type(self.a, self.ho, self.h2, self.Cc)
        if self.flowType == SluiceGateFlowTypes.FreeFlow:
            self.Cq = free_flow_discharge_coefficient(self.a, self.ho)
            self.q = free_flow_discharge(self.a, self.b, self.ho)
        else:
            self.Cq = submerged_flow_discharge_coefficient(self.a, self.ho, self.h2)
            self.q = submerged_flow_discharge(self.a, self.b, self.ho, self.h2)
        return self.q

    def free_flow_ho(self):
        """Solves free flow upstream depth with the given values of q, a and b
        """
        self.ho = fsolve(lambda ho: self.q - free_flow_discharge(self.a, self.b, ho), self.a / 2.0)[0]
        self.Cq = free_flow_discharge_coefficient(self.a, self.ho)
        self.Cc = free_flow_contradiction_coefficient(self.a, self.ho)
        self.h1 = self.Cc * self.a
        self.h1k = self.h1
        self.hcr = critical_depth(self.q, self.b)
        return self.ho

    def submerged_flow_ho(self):
        """Solves submerged flow upstream depth with the given values of q, a, b and h2
        """
        self.ho = fsolve(lambda ho: self.q - submerged_flow_discharge(self.a, self.b, ho, self.h2), self.a / 2.0)[0]
        self.Cq = submerged_flow_discharge_coefficient(self.a, self.ho, self.h2)
        self.Cc = free_flow_contradiction_coefficient(self.a, self.ho)
        self.h1 = self.Cc * self.a
        self.h1k = self.h1
        self.hcr = critical_depth(self.q, self.b)
        return self.ho

def free_flow_contradiction_coefficient(a, ho):
    """Finds free flow contradiction coefficient Cc
    Parameters
    ----------
    a : float
        Gate opening.
    ho : float
        Upstream depth.
    Returns
    -------
    float
        Contradiction coefficient.
    """
    a_ho = [0.0, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85,
            0.90, 0.95, 1.0]
    c_c = [0.611, 0.615, 0.618, 0.620, 0.622, 0.625, 0.628, 0.630, 0.638, 0.645, 0.650, 0.660, 0.675, 0.690, 0.705,
           0.720, 0.745, 0.780, 0.835, 1.000]
    return np.interp(a / ho, a_ho, c_c)

def flow_type(a, ho, h2, cc):
    """Finds flow type.
    Parameters
    ----------
    a : float
        Gate opening.
    ho : float
        Upstream depth.
    h2 : float
        Downstream, tail water depth.
    cc : float
       Contradiction coefficient.
    Returns
    -------
    SluiceGateFlowTypes
        Flow type (Free flow or submerged flow)
    """
    h2_calculated = 0.5 * cc * a * (sqrt(1.0 + 16 * pow(ho / a, 2.0) / (cc * (cc + ho / a))) - 1)
    if h2_calculated > h2:
        return SluiceGateFlowTypes.FreeFlow
    else:
        return SluiceGateFlowTypes.SubmergedFlow

def free_flow_discharge_coefficient(a, ho):
    """Finds free flow type discharge coefficient (Cq).
    Parameters
    ----------
    a : float
        Gate opening.
    ho : float
        Upstream depth.
    Returns
    -------
    float
        Free flow discharge coefficient.
    """
    cc = free_flow_contradiction_coefficient(a, ho)
    cq = cc / sqrt(1 + cc * a / ho)
    return cq

def submerged_flow_discharge_coefficient(a, ho, h2):
    """Finds submerged flow type discharge coefficient (Cq).
    Parameters
    ----------
    a : float
        Gate opening.
    ho : float
        Upstream depth.
    h2 : float
        Downstream, tail water depth.
    Returns
    -------
    float
        Submerged flow discharge coefficient.
    """
    cc = free_flow_contradiction_coefficient(a, ho)
    a_ho = a / ho
    a_h2 = a / h2
    m = 1 - 2.0 * cc * a_ho / (1 + cc * a_ho) + (2 * pow(cc, 2.0) * a_ho / (1 + cc * a_ho)) * a_h2
    k = sqrt(m - sqrt(pow(m, 2.0) - 1 + pow(h2 / ho, 2.0)))
    cq = free_flow_discharge_coefficient(a, ho)
    return k * cq

def free_flow_discharge(a, b, ho):
    cq = free_flow_discharge_coefficient(a, ho)
    q = cq * a * b * sqrt(2.0 * g * ho)
    return q

def submerged_flow_discharge(a, b, ho, h2):
    cq = submerged_flow_discharge_coefficient(a, ho, h2)
    q = cq * a * b * sqrt(2.0 * g * ho)
    return q

def critical_depth(q, b):
    return pow(pow(q, 2.0) / (pow(b, 2.0) * g), 1.0 / 3.0)

sg = SluiceGate(a=0.90, b=3.0, ho=5.4, h2=3.6)
print('Q =', sg.q)
print('Cc =', sg.Cc)
print('Cq =', sg.Cq)
print('h1k =', sg.h1k)
print('h2k =', sg.h2k)
print('Akım Tip =', sg.flowType)
    Q = 10.98409295919213
    Cc = 0.6186666666666667
    Cq = 0.3953012794655725
    h1k = 0.5568000000000001
    h2k = 1.9549092928224936
    Akım Tip = SluiceGateFlowTypes.SubmergedFlow

Yorum yapın

Bunlar ilginizi çekebilir:

Dönüşüm Matrisleri

AutoCAD.Net API ile dönüşüm matrisleri (ölçekleme, döndürme, yer değiştirme).

USBR Tip Enerji Kırıcı Havuzlar

Enerji kırıcı havuzlar, yüksek hıza sahip akımların aşındırıcı etkisini azaltmak için dolusavak, tünel/konduvi, menfez vb. hidrolik yapıların çıkışlarında ku...