USBR Tip Enerji Kırıcı Havuzlar
Enerji kırıcı havuzlar, yüksek hıza sahip akımların aşındırıcı etkisini azaltmak için dolusavak, tünel/konduvi, menfez vb. hidrolik yapıların çıkışlarında kullanılır. Enerjiyi kırarak dere yatağını korur ve yapı civarında oyulmaları önlerler.
Enerji kırıcı havuzların hidrolik tasarımındaki prensip kuyruk suyu derinliğininin kontrol edilerek hidrolik sıçramanın yapı içinde oluşmasını sağlamaya dayanır. Bu yapıların geometrik boyutları gelen akımın derinliğine ve hızına, dolaysıyla froude sayısına bağlıdır.
Hidrolik sıçramanın kırılacak enerji ile akım derinliğinin ilişkisine bağlı olarak farklı biçimleri vardır. “Bureau of Reclamation” 1 tarafından hidrolik sıçramanın özelliklerini belirlemek için model deneyleri gerçekleştirilmiş ve çeşitli Froude sayısı aralıklarına göre hidrolik sıçrama sınıflandırılmıştır.
Sıçrama Türleri
$1.00 \lt F_{r1} \lt 1.7$ Dalgalı Sıçrama
Froude sayısı birim ya da akım kritikten akarken hidrolik sıçrama oluşmaz. Eşlenik derinlikler $d_1$ ve $d_2$ arasındaki fark az olduğundan su yüzünde sadece hafif bir dalgalanma gözlenir.
$1.70 \lt F_{r1} \lt 2.5$ Zayıf Sıçrama
Froude sayısının 1.70’yi aşmasıyla birlikte su yüzeyinde bir takım küçük çalkantılar oluşur ve bu durum 2.5 değerine ulaşana kadar kuvvetlenerek artar. Ancak hidrolik sıçramanın davranışında bir değişiklik olmaz. Mansapta su yüzeyi düzgün kalır ve zayıf sıçrama oluşur.

$2.5 \lt F_{r1} \lt 4.5$ Salınımlı Sıçrama
Salınımlı bir su jeti tabandan yüzeye ve tekrar tabana doğru düzensiz bir şekilde hareket eder. Her salınım yüzeyde büyük ve düzensiz dalgalar oluşturur. Bu dalgalar ancak uzun mesafeler sonunda sönümlenir ve salınımlı sıçrama oluşur.
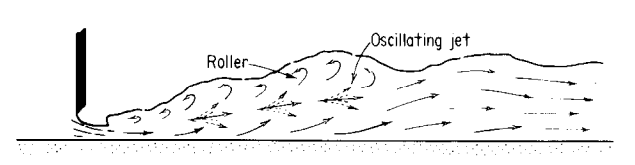
$4.5 \lt F_{r1} \lt 9.0$ Kararlı Sıçrama
Yüksek hızlı su jeti sürekli aynı yolu izler. Bu sıçrama tipi mansap etkilerinden en az etkilenen tiptir. Kararlı sıçrama oluşur.

$F_{r1} \gt 9.0$ Kuvvetli Sıçrama
Yüksek hızlı jet sıçramanın ön yüzünde darbe etkileri yaratır ve mansapta dalgalı bir yüzey oluşturur. Sıçrama kuvvetlidir.

Enerji Kırıcı Havuz Tipleri
USBR Tip-I $(1.7 \lt Fr_{1} \lt 2.5)$
Tip-I, şüt bloğu, şaşırtıcı/sönümleyici blok ve mansap eşiği içermez. Havuz boyunun uzun olması ve hidrolik sıçramanın mansap su seviyesi değişimine karşı duyarlı olması nedeniyle genellikle tercih edilmez. Havuz boyu $L$ havuz sonundaki eşlenik derinliğe $d_2$ bağlı olarak (1) eşitliği ile bulunabilir.2
\[L/d_{2} = −0.00005 \times Fr_{1}^3 − 0.0036 \times Fr_{1}^2 + 0.0816 \times Fr_{1} + 5.6544 \tag{1}\]USBR Tip-IV $(2.5 \lt Fr_{1} \lt 4.5)$
Bu tip salınımlı sıçramalar için geliştirilmiştir. Salınımın kararsızlığını azaltmak için şüt saptırma blokları ve mansap eşiği barındırır. Havuz boyu (2) eşitliği ile bulunabilir. Kuyruk suyu derinliğinin eşlenik derinlikten $d_2$ %10 kadar fazla olması önerilmektedir. Çünkü hidrolik sıçrama, düşük Froude sayılarında, kuyruk suyu derinliğine karşı duyarlıdır ve kuyruk suyu derinliğindeki küçük bir azalma sıçramanın havuz dışına taşınmasına neden olabilir.3
\[L/d_2 = 0.0411 \times Fr_1^3 − 0.5838 \times Fr_1^2 + 3.0198 \times Fr_1 + 0.3164 \tag{2}\]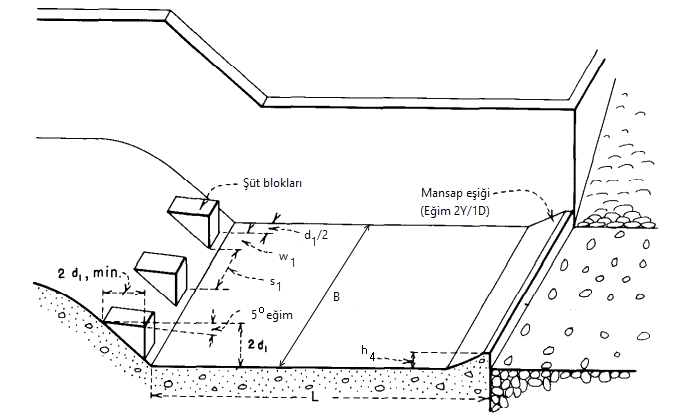
Blok genişliği, $0.75\le w_{1}/d_{1}\le 1$ olmak koşuluyla, $w_{1}=B/3.5$ ve blok aralığı ise $s_{1}=2.5\times w_{1}$ seçilebilir. Mansap eşiği yüksekliği ise $h_{4}=d_{1}\times (0.0536\times Fr_{1}+1.04)$ eşitliğiyle hesaplanabilir.
USBR Tip-II $(Fr_{1} \gt 4.5 \; ; V_{1} \gt 18\,m/s$)
Bu tip, yüksek barajlar, dolgu baraj dolusavakları ve büyük kanal yapıları için geliştirilmiştir. Tasarım şüt bloklarını ve dişli mansap eşiğini içerir. klasik bir hidrolik sıçramayla karşılaştırıldığında gerekli havuz boyunu %30 azaltır. Akımın yüksek hızları düşünülerek şaşırtıcı blok yerleştirilmemiştir. Aynı nedenle kuyruk suyu derinliğinin eşlenik derinlikden $d_2$ %5 kadar fazla olması önerilmektedir. Havuz boyu $L$ (3) eşitliği ile bulunabilir.
\(L/d_{2} = 0.0009 \times Fr_{1}^3 − 0.0385 \times Fr_{1}^2 + 0.5328 \times Fr_{1} + 1.9551 \tag{3}\) %5 güvenlik faktörüyle kuyruk suyu derinliği için (4) eşitliği kullanılabilir.
\[TW=0.475\times d_{1} \times\left(\sqrt{1+8\times Fr_{1}^2} -1\right)\tag{4}\]
Şüt blokları sayısı, $n_{sb}=B/(2 \times d_1)$, $\;w_{1}=s_{1}=B/(2 \times n_{sb})$ olarak seçilebilir. Masap eşiği yüksekliği $h_{2}=0.2\times d_{2}$ olmalı ve aralığı ise $s_{2}=0.15\times d_{2}$’den az olmamalıdır. Diş adedi $\;B/(0.30\times d_{2})+0.50$ eşitliğiyle hesaplanabilir.
USBR Tip-III $(Fr_{1} \gt 4.5 \; ; V_{1} \lt 18.3\,m/s\; ; q \lt 18.6\,m^{3}/s/m$)
Bu tip de Tip-II gibi yüksek barajlar, dolgu baraj dolusavakları ve büyük kanal yapıları için geliştirilmiştir. Tasarım şüt bloklarını, şaşırtıcı bloklar ve mansap eşiği içerir. Klasik hidrolik sıçramayla karşılaştırıldığında havuz boyunu %45 azaltır. Akımın hızları sınırlandırılarak beton yüzeyde kavitasyon hasarının önüne geçilmeye çalışılmış ve şaşırtıcı bloklara etkiyen çarpma kuvvetleri azaltılmıştır. Havuz boyu (5) eşitliği ile bulunabilir. Şaşırtıcı blokların havuz başlangıcından uzaklığı $0.8\times d_{2}$ olmalıdır.
\[L/d_{2} = 0.0005 \times Fr_{1}^3 − 0.0222 \times Fr_{1}^2 + 0.3271 \times Fr_{1} + 1.1558 \tag{5}\]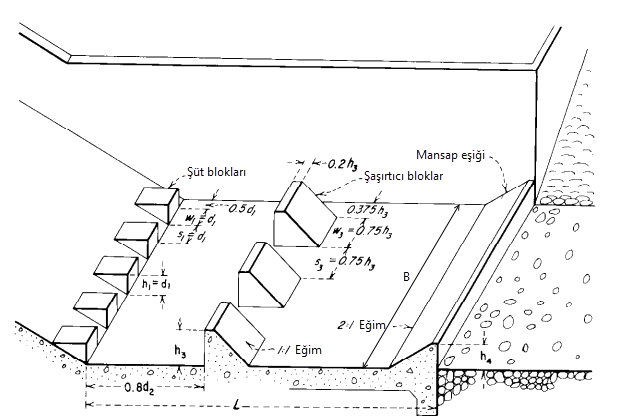
Şüt blokları yüksekliği $(h_{3}$) için eşitlik (6), mansap eşiği yüksekliği $(h_{4}$) için ise eşitlik (7) kullanılabilir. Sıçramanın havuz içinde gerçeklemesi için ise kuyruk suyu derinliği en az $0.832\times d_{2}$ olmalıdır.
\[h_{3}=d_{1}\times (0.175 \times Fr_{1}+0.6)\tag{6}\] \[h_{4}=d_{1}\times (0.0571 \times Fr_{1}+0.9714)\tag{7}\]Python Kodu
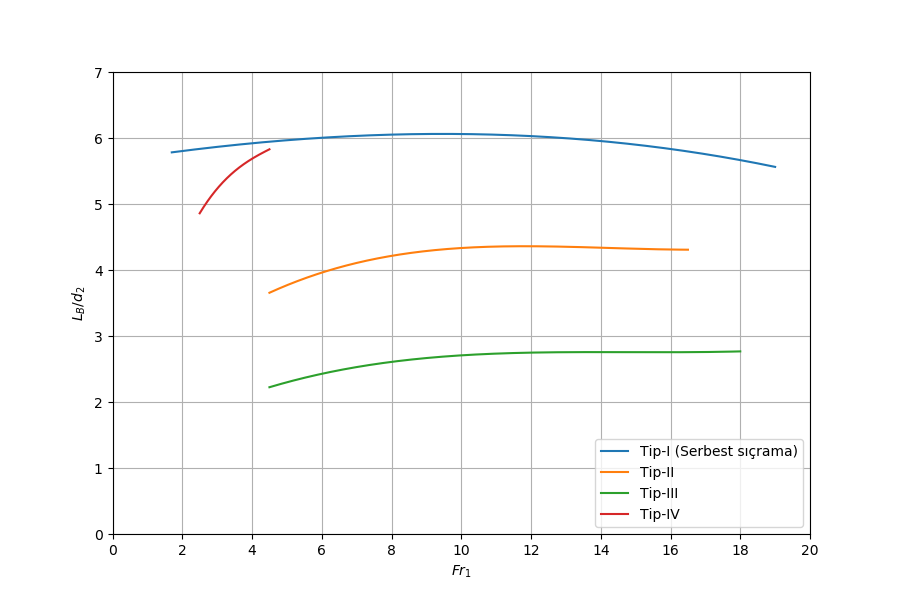
USBR tipi dört enerji kırıcı havuzun boylarının Froude sayısı ile değişimini birlikte gösteren grafik Şekil-8’de verilmiştir. Bu grafiği çizdirmek için usbr_type_stilling_basin_graph() python yordamı kullanılmıştır.
import numpy as np
import matplotlib.pyplot as plt
def usbr_type_stilling_basin_graph():
def Ld2(fr1, usbr_type):
if usbr_type == "I":
return -5e-5 * pow(fr1, 3.0) - 0.0036 * pow(fr1, 2.0) + 0.0816 * fr1 + 5.6544
elif usbr_type == "II":
return 9e-4 * pow(fr1, 3.0) - 0.0385 * pow(fr1, 2.0) + 0.5328 * fr1 + 1.9551
elif usbr_type == "III":
return 5e-4 * pow(fr1, 3.0) - 0.0222 * pow(fr1, 2.0) + 0.3271 * fr1 + 1.1558
else:
return 0.0411 * pow(fr1, 3.0) - 0.5838 * pow(fr1, 2.0) + 3.0198 * fr1 + 0.3164
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(111)
ax.set_xlabel('$Fr_1')
USBR tip enerji kırıcı havuz boyutlarını hesaplamak için ise aşağıdaki USBRStillingBasin python sınıfı kullanılabilir.
from math import sqrt
from scipy.constants import g
import numpy as np
import matplotlib.pyplot as plt
class USBRStillingBasin:
"""
Stilling basin object
Attributes
----------
q : float
Discharge (m3/s)
b : float
Basin width (m)
d1 : float
Upstream conjugate depth (m)
d2 : float
Downstream conjugate depth (m)
dc : float
Critical depth (m)
d3 : float
Tail water depth (m)
v3 : float
Downstream channel velocity (m)
k1 : float
Basin elevation (m)
k2 : float
Downstream channel elevation (m)
"""
def __init__(self, q, b, d1, d3, v3, k1, k2):
self.q = q
self.b = b
self.d1 = d1
self.d3 = d3
self.k1 = k1
self.k2 = k2
self.v3 = v3
self.v1 = q / (b * d1)
self.fr1 = self.v1 / sqrt(g * d1)
self.d2 = 0.5 * d1 * (sqrt(1 + 8 * pow(self.fr1, 2.0)) - 1.0)
self.v2 = q / (b * self.d2)
self.dc = pow(pow(q / b, 2.0) / g, 1.0 / 3.0)
self.vc = q / (b * self.dc)
self.e1 = k1 + self.d1 + pow(self.v1, 2.0) / (2 * g)
self.e2 = k1 + self.d2 + pow(self.v1, 2.0) / (2 * g)
self.e3 = k2 + self.d3 + pow(self.v3, 2.0) / (2 * g)
self.ec = k2 + self.dc + pow(self.vc, 2.0) / (2 * g)
self.unit_q = q / b
self.lb = 0.0
self.s1 = self.w1 = self.s2 = self.w2 = self.s3 = self.w3 = 0.0
self.h1 = self.h2 = self.h3 = self.h4 = 0.0
self.min_d3 = 0.0
if 1.7 <= self.fr1 < 2.5: # Type-I
self.basin_type_1()
self.type = "I"
elif 2.5 <= self.fr1 < 4.5: # Type-IV
self.basin_type_4()
self.type = "IV"
elif self.fr1 >= 4.5 and self.v1 > 18.0: # Type-II
self.basin_type_2()
self.type = "II"
self.min_d3 = 1.05 * self.d2
else: # Type-III
self.basin_type_3()
self.type = "III"
self.min_d3 = 0.832 * self.d2
def basin_type_1(self):
l_d2 = -5e-5 * pow(self.fr1, 3.0) - 0.0036 * pow(self.fr1, 2.0) + 0.0816 * self.fr1 + 5.6544
self.lb = l_d2 * self.d2
def basin_type_2(self):
l_d2 = 9e-4 * pow(self.fr1, 3.0) - 0.0385 * pow(self.fr1, 2.0) + 0.5328 * self.fr1 + 1.9551
self.lb = l_d2 * self.d2
self.h1 = self.d1
self.h2 = 0.2 * self.d2
self.s1 = self.w1 = self.d1
self.s2 = self.w2 = 0.15 * self.d2
def basin_type_3(self):
l_d2 = 5e-4 * pow(self.fr1, 3.0) - 0.0222 * pow(self.fr1, 2.0) + 0.3271 * self.fr1 + 1.1558
self.lb = l_d2 * self.d2
self.h1 = self.d1
self.h3 = self.d1 * (0.175 * self.fr1 + 0.60)
self.h4 = self.d1 * (0.0571 * self.fr1 + 0.9714)
self.s1 = self.w1 = self.d1
self.s3 = self.w3 = 0.75 * self.h3
def basin_type_4(self):
l_d2 = 0.0411 * pow(self.fr1, 3.0) - 0.5838 * pow(self.fr1, 2.0) + 3.0198 * self.fr1 + 0.3164
self.lb = l_d2 * self.d2
self.h1 = self.d1
self.h2 = 0.2 * self.d2
self.w1 = self.b / 3.5
if self.w1/self.d1 < 0.75:
self.w1 = 0.75 * self.d1
elif self.w1/self.d1 > 1.0:
self.w1 = self.d1
self.s1 = 2.5 * self.w1
self.h4 = self.d1 * (0.0536 * self.fr1 + 1.04)
Örnek Çözüm
basin = USBRStillingBasin(14.82, 9.5, 0.22, 1.19, 1.31, 1153.30, 1153.70)
print("Tip =", basin.type)
print("L = {0:.2f} m".format(basin.lb))
print("Fr1 = {0:.2f}".format(basin.fr1))
print("d1 = {0:.2f} m, d2 = {1:.2f} m, d3 = {2:.2f} m".format(basin.d1, basin.d2, basin.d3))
print("Minimum d3 = {0:.2f} m".format(basin.min_d3))
print("dc = {0:.2f} m".format(basin.dc))
print("V1 = {0:.2f} m/s, V2 = {1:.2f} m/s".format(basin.v1, basin.v2))
if basin.type == "II":
print("h1 = s1 = w1 = {0:.2f} m".format(basin.d1))
print("h2 = {0:.2f} m".format(basin.h2))
print("s2 = w2 = {0:.2f} m".format(basin.s2))
elif basin.type == "III":
print("h3 = {0:.2f} m, h4 = {1:.2f} m".format(basin.h3, basin.h4))
print("h1 = s1 = w1 = {0:.2f} m".format(basin.d1))
print("s3 = w3 = {0:.2f} m".format(basin.s3))
elif basin.type == "IV":
print("s1 = {0:.2f} m".format(basin.s1))
print("h4 = {0:.2f} m".format(basin.h4))
print("w1= {0:.2f} m".format(basin.w1))
Tip = III
L = 3.17 m
Fr1 = 4.83
d1 = 0.22 m, d2 = 1.40 m, d3 = 1.19 m
Minimum d3 = 1.16 m
dc = 0.63 m
V1 = 7.09 m/s, V2 = 1.12 m/s
h3 = 0.32 m, h4 = 0.27 m
h1 = s1 = w1 = 0.22 m
s3 = w3 = 0.24 m
-
BUREC (1980). Hydraulic Design of Stilling Basins and Energy Dissipators. Water Resources Publications, U.S. Dept.of Interior, Bureau of Reclamation, Denver. ↩
-
Hubert Chanson (2015). Energy Dissipation in Hydraulic Structures. CRC Press ↩
-
Kazım Çeçen (1982). Açık Kanallar, Hidrolik, Cilt II. İTÜ Yayınları. ↩

Yorum yapın