Shields Eğrisinin Matematiksel İfadesi

Sediment taşınımında kullanılan Shields eğrisi Şekil-1‘de verilmiştir.

Şekil-1

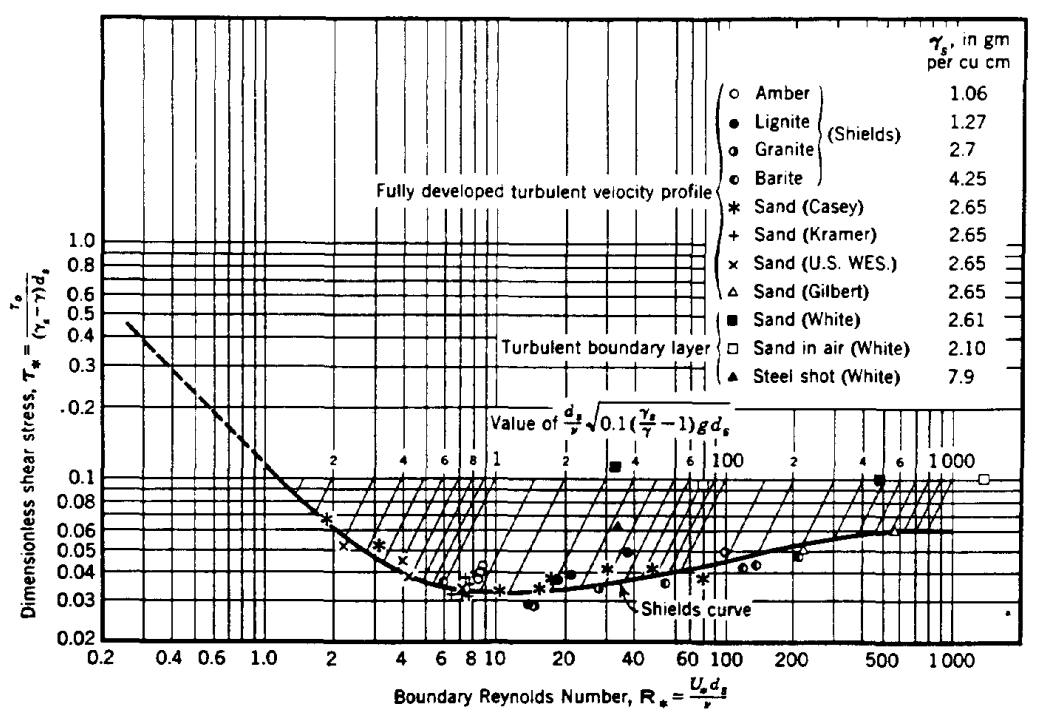
Deneysel çalışmalar sonucu elde edilen bu eğri boyutsuz kayma gerilmesi ($\tau_{\ast c}$) ve reynolds sayısına ($Re_{\ast c}$) göre hazırlanmıştır.

\[\tau_{*c}=\dfrac{\tau_c}{\left(\dfrac{\rho_s}{\rho}-1\right)\times \rho\times g\times d}\tag{1}\] \[Re_{*c}= \dfrac{u_{*c}\times d}{\upsilon}\tag{2}\]

$\tau_c:$ Kritik kayma gerilmesi.

$\tau_{*c}:$ Boyutsuz kritik kayma gerilmesi.

$\rho_s:$ Sediment özgül kütlesi.

$\rho:$ Su özgül kütlesi $(9.81\;kN/m^3 \approx 1.00\;t/m^3$).

$\gamma:$ Suyun özgül ağırlığı.

$\upsilon:$ Suyun kinematik viskozitesi.

$g:$ Yerçekimi ivmesi.

$d:$ Dane çapı.

$u_{*c}:$ Kritik sürüklenme hızı.

Su için kinematik viskozite sıcaklığa bağlı olarak Eşitlik-3 ya da Eşitlik-4 ile hesaplanabilir.

\[\upsilon=10^{-6}\times[1.7688+(0.659\times 10^{-3}\times (T-1)-0.05076)\times (T-1)]\tag{3}\]

\(\upsilon=\dfrac{1.792\times 10^{-6}}{1+\left(\dfrac{T}{25}\right)^{1.165}}\tag{4}\) Burada $\upsilon, \space m^2/s$, $T$ ise $^oC$ ‘dir.

def kinematic_viscosity(t=10):
    return 1.792e-6 / (1 + pow(t / 25, 1.165))

Shields eğrisinden kritik kayma gerilmesi ve sürüklenme hızlarının hesabı için shields sayısının, boyutsuz dane çapı $(d_*$) ile ifade edildiği Eşitlik-5 ve Eşitlik-6 kullanılabilir.¹

\(\tau_{*c}=\dfrac{0.23}{d_*}+0.054\left[ 1-exp\left( -\dfrac{d_{*}^{0.85}}{23}\right)\right]\tag{5}\) \(d_*=\left[\dfrac{\left(\dfrac{\rho_s}{\rho}-1\right)\times g}{\upsilon^2}\right]^{1/3}\times d \tag{6}\)

Shields eğrisinin matematiksel olarak ifadesi için aşağıdaki yordam oluşturulmuştur.

def shields_curve_equation(d, r_p=2.65, r_w=1.0, v=1.40e-6):
    """
    Calculates shields curve equation mathematically.
    :param d: Particle diameter [m]
    :param r_p: Density of particle [t/m3]
    :param r_w: Density of water [t/m3]
    :param v: Kinematic viscosity [m2/s]
    :return: array of (critical shields number, critical shear stress, shear velocity, reynolds number)
    """
    dimensionless_dia = pow((r_p / r_w - 1.0) * g / pow(v, 2.0), 1.0 / 3.0) * d
    critical_shields_number = 0.23 / dimensionless_dia + 0.054 * (1.0 - exp(-pow(dimensionless_dia, 0.85) / 23.0))
    critical_shear_stress = critical_shields_number * (r_p / r_w - 1.0) * g * r_w * d
    shear_velocity = sqrt(critical_shear_stress / r_w)
    reynolds_number = shear_velocity * d / v
    return critical_shields_number, critical_shear_stress, shear_velocity, reynolds_number

Örnek

$T=10^o$ için kinematic_viscosity(...) yordamıyla kinematik viskozite $\upsilon= 1.333458e^{-6}\;m^2/s$ olarak bulunur.

$\rho_s=2.65\;t/m^3$, $\rho=1.0\;t/m^3$ özgül kütleleri ve dane çapı $d=1\;mm$ için shields_curve_equation(0.001, 2.65, 1.00, 1.33345e-6) python yordamı ile aşağıdaki sonuçlar hesaplanmıştır.

$\tau_{\ast c}=0.034643$, $\tau_{c}=0.0005605\;t/m^2$, $u_{\ast c}=0.023676\;m/s$, $Re_{\ast c}=17.75576$

Shields Eğrisinin Çizdirilmesi

def shields_diagram(r_p=2.65, r_w=1.0, v=1.40e-6):
    diameters = np.linspace(0.01, 100.0, 2000, dtype=np.float)
    print(diameters)
    critical_shields_number = np.fromiter((shields_curve_equation(d / 1000.0, r_p, r_w, v)[0] for d in diameters),
                                          np.float)
    reynolds_number = np.fromiter((shields_curve_equation(d / 1000.0, r_p, r_w, v)[3] for d in diameters), np.float)
    fig, ax = plt.subplots()
    ax.set_xlabel(r'$Reynolds\;Sayısı\;[Re_{*c}]$')
    ax.set_ylabel(r'$Shields\;Sayısı\;[\tau_{*c}]$')
    ax.loglog(reynolds_number, critical_shields_number, basex=10)
    ax.grid(True, which='both')
    ax.set_ylim(bottom=0.01)
    ax.set_ylim(top=1.0)
    ax.set_xlim(left=0.1)
    ax.set_xlim(right=1000.0)
    plt.show()

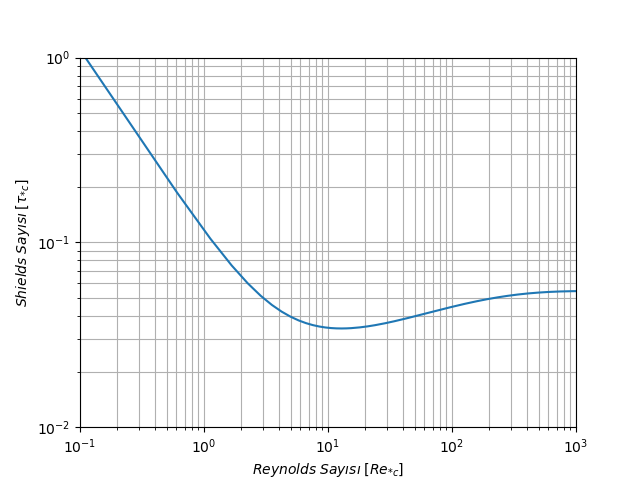
$\upsilon= 1.333458e^{-6}\;m^2/s$, $\rho_s=2.65\;t/m^3$, $\rho=1.0\;t/m^3$ için Shields eğrisi Şekil-2‘de verilmiştir.

shields_diagram(2.65, 1.00, 1.33345e-6)

Şekil-2

Dane Çapı-Kritik Kayma Gerilmesi ve Dane Çapı-Kritik Sürüklenme Hızı Eğrileri

def shields_diagram_critical_shear_stress_velocity(r_p=2.65, r_w=1.0, v=1.40e-6):
    diameters = np.linspace(0.01, 100.0, 2000, dtype=np.float)
    shear_stress = np.fromiter((shields_curve_equation(d / 1000.0, r_p, r_w, v)[1] * g * 1000 for d in diameters),
                               np.float)
    shear_velocity = np.fromiter((shields_curve_equation(d / 1000.0, r_p, r_w, v)[2] for d in diameters), np.float)
    fig, ax1 = plt.subplots()
    ax1.set_xlabel('$D\;[mm]$')
    ax1.set_ylabel('$u_{*c}\;[m/s]$')
    ax1.loglog(diameters, shear_velocity, basex=10, color='r', linestyle='--', label='$u_{*c}$')
    ax1.tick_params(axis='y')
    ax1.grid(True, which='major')
    ax1.grid(True, which='minor')
    ax1.set_ylim(bottom=0.001)
    ax1.set_ylim(top=1.0)
    ax1.legend(loc=2)

    ax2 = ax1.twinx()
    ax2.set_ylabel(r'$\tau_{*c}\,[\dfrac{N}{m^2}]$')
    ax2.loglog(diameters, shear_stress, basex=10, label=r'$\tau_{*c}$')
    ax2.tick_params(axis='y')
    ax2.set_ylim(bottom=1.0)
    ax2.set_ylim(top=1000.0)
    ax2.legend(loc=4)
    fig.tight_layout()
    plt.title('test')
    plt.show()

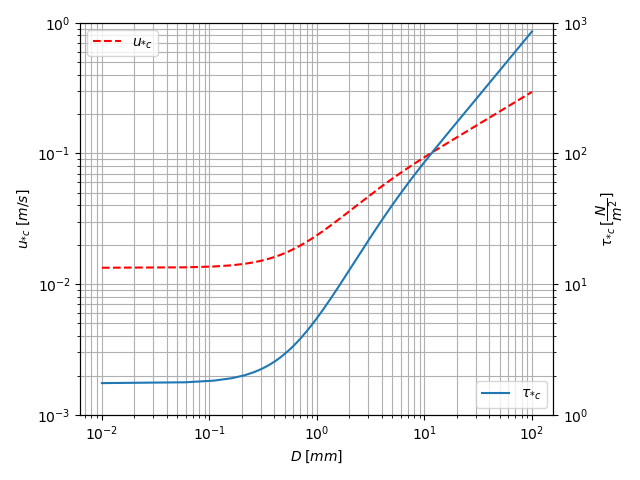
$\upsilon= 1.333458e^{-6}\;m^2/s$, $\rho_s=2.65\;t/m^3$, $\rho=1.0\;t/m^3$ için eğriler Şekil-3‘de verilmiştir.

shields_diagram_critical_shear_stress_velocity(2.65, 1.00, 1.33345e-6)

Şekil-3

1. Gua, Junke (2002).Advances in Hydraulics and Water Engineering, Proc. 13th Iahr-Apd Congress, Vol.2, Hunter Rose and Shields Diagram. ↩