Dairesel Kesitlerin Hidroliği

Açık kanallar için Manning eşitliği,$R$ hidrolik yarıçap, $S_o$) kanal taban eğimi olmak üzere aşağıdaki gibidir. \(Q=V \cdot A =\dfrac{1}{n} \cdot A \cdot R^{2/3} \cdot S_{o}^{1/2}\)

$\beta = 2 \cdot acos(1-2 \cdot \dfrac{h}{D})$ için;

ıslak alan $A=\dfrac {D^{2}} {8}\cdot (\beta - sin(\beta ))$,

ıslak çevre $P=D \cdot \beta /2$,

su yüzü genişliği ise $T=D \cdot sin(\beta /2)$ eşitlikleri ile hesaplanabilir.

Hidrolik yarıçap ise kesit alanının ıslak çevreye oranıdır, $R=\dfrac{A}{P}$

Aşağıda kodlarını bulabileceğiniz Python sınıfı üniform ve kritik akım koşullarında dairesel kesitli kanalların hidrolik özelliklerini hesaplayabilmek için geliştirilmiştir.

from abc import ABCMeta, abstractmethod
from math import pow, sqrt, sin, acos
from scipy.misc import derivative
from scipy.optimize import fsolve, root
import copy
import matplotlib.pyplot as plt
import numpy as np
g = 9.806

class HydraulicProperties(object):
    __metaclass__ = ABCMeta

    def __init__(self, Q=0.0, So=0.0, n=0.0):
        # Flow discharge [m³/sn]
        self.Q = Q
        # Slope of channel bottom [m/m]
        self.So = So
        # Manning coefficient
        self.n = n
        # Water height [m]
        self.h = 0.0
        # Flow cross-sectional area [m²]
        self.A = 0.0
        # Top width of the water surface [m]
        self.T = 0.0
        # Wetted perimeter [m]
        self.P = 0.0
        # Hydraulic radius of the flow cross-section [m]. (A/P)
        self.R = 0.0
        # Flow velocity [m/s]
        self.V = 0.0
        # Froude number
        self.Fr = 0.0
        # Velocity head [m]. (V^2/2g)
        self.hv = 0.0
        # Specific energy [m]. (h+hv)
        self.E = 0.0
        # Hydraulic mean depth [m]. (A/T)
        self.Dm = 0.0
        # Water surface center of gravity [m]
        self.Z = 0.0
        # Momentum [m³]. (Q^2/g.A + Z.A)
        self.M = 0.0

    @abstractmethod
    def calculate_hydraulic_properties(self, y):
        raise NotImplementedError('You need to define a "_calculate_hydraulic_properties" method!')

    def __uniform_water_height(self, y):
        self.calculate_hydraulic_properties(y)
        return self.Q - self.A * pow(self.R, 2.0 / 3.0) * pow(self.So, 0.5) / self.n

    def __critical_water_height(self, y):
        self.calculate_hydraulic_properties(y)
        return sqrt(g * pow(self.A, 3.0) / self.T) - self.Q

    def get_uniform_properties(self):
        self.h = fsolve(self.__uniform_water_height, 0.001)
        return copy.deepcopy(self)

    def get_critical_properties(self):
        self.h = fsolve(self.__critical_water_height, 0.001)
        return copy.deepcopy(self)

class CircularShapeProperties:
    def __init__(self, D=0.0):
        # Diameter of flow section (m)
        self.D = D
        self.beta = 0.0

class CircularSection(HydraulicProperties, CircularShapeProperties):
    def __init__(self, Q, So, n, D, h=0.00):
        CircularShapeProperties.__init__(self, D)
        HydraulicProperties.__init__(self, Q, So, n)
        if h != 0.00 and Q == 0.00:
            self.h = h
            self.Q = self.calculate_discharge(h)
            self.calculate_hydraulic_properties(h)

        if Q > self.calculate_maximum_discharge_depth()[1]:
            raise ValueError('Q > Qmax')

    def calculate_hydraulic_properties(self, y):
        self.beta = 2.0 * acos(1.0 - 2.0 * y / self.D)
        self.A = pow(self.D, 2.0) * (self.beta - sin(self.beta)) / 8.0
        self.T = self.D * sin(self.beta / 2.0)
        self.P = self.D * self.beta / 2.0
        self.R = self.A / self.P
        self.Dm = self.A / self.T
        self.V = self.Q / self.A
        self.hv = pow(self.V, 2.0) / (2.0 * g)
        self.E = y + self.hv
        self.Fr = self.V / sqrt(g * self.A / self.T)
        self.Z = self.D / 2.0 - 2.0 * pow(y * self.D - pow(y, 2.0), 1.50) / (3.0 * self.A)
        self.M = pow(self.Q, 2.0) / (g * self.A) + self.Z * self.A

    def calculate_discharge(self, y):
        self.beta = 2.0 * acos(1.0 - 2.0 * y / self.D)
        self.A = pow(self.D, 2.0) * (self.beta - sin(self.beta)) / 8.0
        self.P = self.D * self.beta / 2.0
        self.R = self.A / self.P
        return self.A * pow(self.R, 2.0 / 3.0) * pow(self.So, 0.5) / self.n

    def calculate_maximum_discharge_depth(self):
        h = root(lambda y: derivative(self.calculate_discharge, y, dx=1e-6), 0.95 * self.D, method='lm').x[0]
        return h, self.calculate_discharge(h)

    def calculate_full_discharge(self):
        return self.calculate_discharge(self.D)

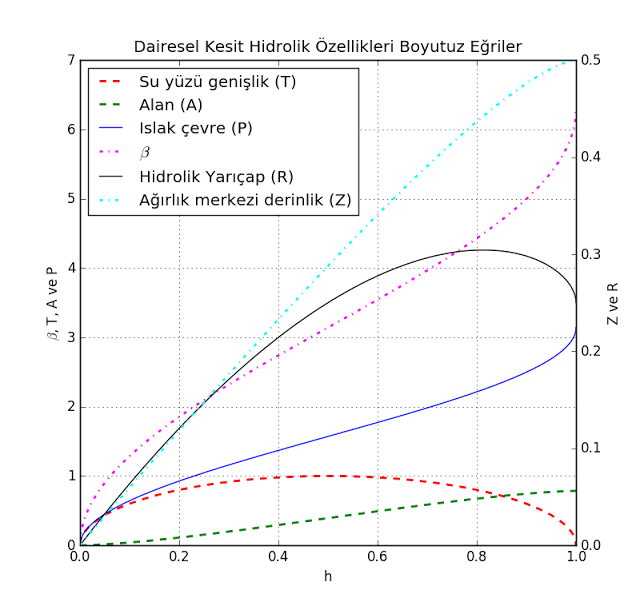
draw_non_dimensional_circular_section(…) yordamı ile dairesel kesitlerin boyutsuz hidrolik özelliklerini elde edebilirsiniz.

def draw_non_dimensional_circular_section(file_path=None):
    d, n, So, Q = 1.0, 0.014, 0.001, 0.0
    p, t, a, z, r, beta = [], [], [], [], [], []
    h_ = np.linspace(0.0001, d, 1000)
    for val in h_:
        sect = CircularSection(Q, So, n, d, h=val)
        sect.calculate_hydraulic_properties(val)
        p.append(sect.P)
        t.append(sect.T)
        z.append(sect.Z)
        a.append(sect.A)
        r.append(sect.R)
        beta.append(sect.beta)
    fig, ax1 = plt.subplots()
    ax2 = ax1.twinx()
    ax1.grid(which='both')
    line1, = ax1.plot(h_, t, color='red', linestyle='--', linewidth=2)
    line2, = ax1.plot(h_, a, color='green', linestyle='--', linewidth=2)
    line3, = ax1.plot(h_, p, color='blue')
    line4, = ax1.plot(h_, beta, color='magenta', linestyle='-.', linewidth=2)
    line5, = ax2.plot(h_, r, color='black')
    line6, = ax2.plot(h_, z, color='cyan', linestyle='-.', linewidth=2)
    ax1.set_xlabel('h')
    ax2.set_ylabel('Z ve R')
    ax1.set_ylabel(r'$\beta$, T, A ve P')
    plt.legend([line1, line2, line3, line4, line5, line6], ['Su yüzü genişlik (T)', 'Alan (A)', 'Islak çevre (P)',
                                                            r'$\beta$', 'Hidrolik Yarıçap (R)',
                                                            'Ağırlık merkezi derinlik (Z)'], loc='best')
    plt.title('Dairesel Kesit Hidrolik Özellikleri Boyutuz Eğriler', verticalalignment='bottom')
    if file_path is not None:
        plt.savefig(file_path, dpi=600, format="png")
    else:
        plt.show()  

Şekil-2

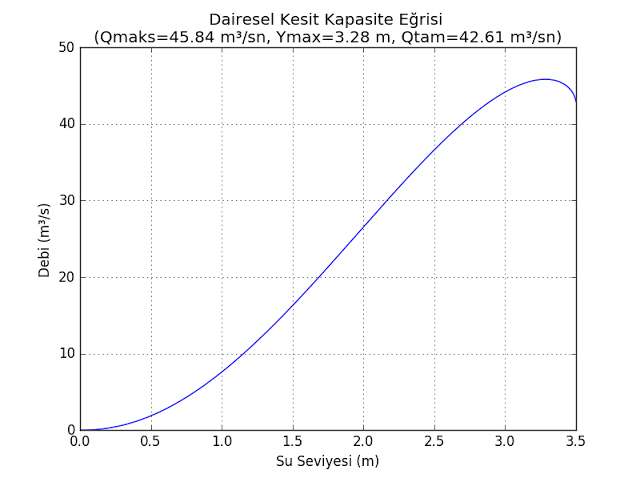
draw_circular_section_rating_curve(…) yordamı ise dairesel kesitlerin kapasite eğrisini çizmekte kullanılabilir.

def draw_circular_section_rating_curve(section: CircularSection, file_path=None):
    tip = 'Dairesel'
    df = lambda y: derivative(section.calculate_discharge, y, dx=1e-6)
    ymax = root(df, 0.95*section.D, method='lm').x[0]
    qmax = section.calculate_discharge(ymax)
    y_arr = np.arange(0.001, section.D, 0.001, np.float)
    q_arr = np.fromiter((section.calculate_discharge(y) for y in y_arr), np.float)
    plt.plot(y_arr, q_arr, linestyle='solid')
    plt.title(tip + ' Kesit Kapasite Eğrisi \n(Qmaks={0:0.2f} m³/sn, Ymax={1:0.2f} m, Qtam={2:0.2f} m³/sn)'.format(qmax, ymax, section.calculate_full_discharge()))
    plt.xlabel('Su Seviyesi (m)')
    plt.ylabel(r'Debi (m³/s)')
    plt.grid(which='both')
    if file_path is not None:
        plt.savefig(file_path, dpi=600, format="png")
    else:
        plt.show() 

Örneğin kanal taban eğimi $0.006 \; m/m$, $n=0.016$, $D=3.5 \; m$ olan bir kanal için kapasite eğrisi aşağıdaki gibi bulunur.

draw_circular_section_rating_curve(CircularSection(10.0, 0.006, 0.016, 3.5))

Şekil-3