Dikdörtgen Tekil Temellerde Taban Gerilmeleri

Eğik eğilme etkisi altındaki dikdörtgen tekil temellerde basınç bölgeleri A, B, C, D ve E olmak üzere 5 farklı bölgeye ayrılabilir. A üçgen, B beşgen, C dikdörtgen (tam), D x yönünde trapez ve E y yönünde trapez basınç bölgeleridir. (Şekil-1) ^{1 2}

Şekil-1: Eksantiriste bölgeleri

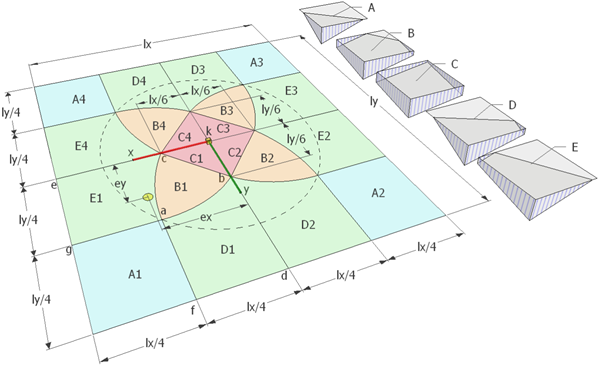
Beşgen basınç bölgesinde $X_n$ ve $Y_n$ değerlerini bulmak için iki değişkenli lineer olmayan bir denklem takımını çözmek gerekmektedir. RectFootingPressDistributionsınıfına ait pentagonal_compression_zone_b ve pentagonal_compression_zone_b_equations yordamları ile bu değerler hesaplanmıştır. Bu değerlerin hesabında SciPy python kütüphanesi fsolve yordamı kullanılmıştır.

RectFootingPressDistribution python sınıfı verili temel boyutları ve kesit tesirleri (M ve N) için aşağıdaki gibidir.

from math import sqrt, fabs, pow
from enum import Enum
from scipy.optimize import fsolve

class EccentricityRegions(Enum):
    """
    Eccentricity regions
    --------------------
    A : enumerate
        Triangular Compression Zone
    B : enumerate
        Pentagonal Compression Zone
    C : enumerate
        Full Compression Zone
    D : enumerate
        Trapezoidal Compression Zone X Direction
    E : enumerate
        Trapezoidal Compression Zone Y Direction
    """
    Null = 1
    A = 2
    B = 3
    C = 4
    D = 5
    E = 6

class RectFootingPressDistribution:
    """
    Rectangular footing base pressure distribution object
    (Determination of base stresses in rectangular footings
    under biaxial bending)
    Attributes
    -------------------------------------------------------
    name : str
           Name of calculation
    p : float
        Axial force
    mx : float
         Bending moment about x axis
    my : float
         Bending moment about y axis
    lx : float
         Footing length in x direction
    ly : float
         Footing length in y direction
    ex : float
         eccentricity of axial load in x direction
    ey : float
         eccentricity of axial load in y direction
    pm : float
         Mean base pressure
    pmax : float
           Maximum base pressure
    pmin : float
           Minimum base pressure
    po, pp, pq, pr : float
                     Actual corner pressures
    p1, p2, p3, p4 : float
                     Rearranged footing corner pressures depending on the eccentricities signs
    xn : float
         Distance of zero pressure point to maximum pressure point (o) in x direction
    yn : float
         Distance of zero pressure point to maximum pressure point (o) in y direction
    xq : float
         Distance of zero pressure point to corner (q) in x direction
    yp : float
         Distance of zero pressure point to corner (p) in y direction
    """
    def __init__(self, name, p, mx, my, lx, ly):

        self.name = name
        self.p = p
        self.mx = mx
        self.my = my
        self.lx = lx
        self.ly = ly
        self.ex = self.my / self.p
        self.ey = self.mx / self.p
        self.kx = fabs(self.ex)/ self.lx
        self.ky = fabs(self.ey) / self.ly
        self.pm = self.p / (self.lx * self.ly)
        self.po = self.pp = self.pq = self.pr = 0.0
        self.pmax = self.pmin = 0.0
        self.xn = self.yn = self.xq = self.yp = 0.0

        self.eccentricity_region = self.find_eccentricity_region()

        if self.eccentricity_region == EccentricityRegions.A:
            self.triangular_compression_zone_a()
        elif self.eccentricity_region == EccentricityRegions.B:
            self.pentagonal_compression_zone_b()
        elif self.eccentricity_region == EccentricityRegions.C:
            self.full_compression_zone_c()
        elif self.eccentricity_region == EccentricityRegions.D:
            self.trapezoidal_compression_zone_x_direction_d()
        elif self.eccentricity_region == EccentricityRegions.E:
            self.trapezoidal_compression_zone_y_direction_e()

        self.p1, self.p2, self.p3, self.p4 = self.corner_pressures()

    def find_eccentricity_region(self):
        x4 = 1.0 + 4.0 * self.kx
        y4 = 1.0 + 4.0 * self.ky
        x12 = sqrt(1.0 - 12.0 * pow(self.kx, 2.0))
        y12 = sqrt(1.0 - 12.0 * pow(self.ky, 2.0))
        c12 = 0.50
        c16 = 1.0 / 6.0
        c14 = 0.25
        eccentricity_region = EccentricityRegions.Null
        if self.kx >= 0.25 and self.kx < 0.5 and self.ky >= 0.25 and self.ky < 0.5:
            eccentricity_region = EccentricityRegions.A
        elif self.kx + self.ky >= c16 and self.kx <= c12 - c16 * (2.0 - y12) * (1.0 + 2.0 * self.ky + y12) / y4 and \
                self.ky <= c12 - c16 * (2.0 - x12) * (1.0 + 2.0 * self.kx + x12) / x4:
            eccentricity_region = EccentricityRegions.B
        elif self.kx + self.ky <= c16:
            eccentricity_region = EccentricityRegions.C
        elif self.kx >= 0 and self.kx <= c14 and self.ky < c12 and \
                self.ky >= c12 - c16 * (2.0 - x12) * (1.0 + 2.0 * self.kx + x12) / x4:
            eccentricity_region = EccentricityRegions.D
        elif self.ky >= 0 and self.ky <= c14 and self.kx < c12 and \
                self.kx >= c12 - c16 * (2.0 - y12) * (1.0 + 2.0 * self.ky + y12) / y4:
            eccentricity_region = EccentricityRegions.E
        return eccentricity_region

    def triangular_compression_zone_a(self):
        self.xn = 4 * self.lx * (0.5 - self.kx)
        self.yn = 4 * self.ly * (0.5 - self.ky)
        self.po = self.pmax = 3.0 * self.pm / (8.0 * (0.5 - self.kx) * (0.5 - self.ky))
        self.pr = self.pp = self.pq = self.pmin = 0.0

    def pentagonal_compression_zone_b(self):
        self.xn, self.yn = fsolve(self.pentagonal_compression_zone_b_equations, (self.lx, self.ly))
        self.yp = self.yn * (1.0 - self.lx / self.xn)
        self.xq = self.xn * (1.0 - self.ly / self.yn)

        self.po = self.pmax = 6.0 * self.pm * self.lx * self.ly / (self.xn * self.yn) / \
                              (1.0 - pow(1.0 - self.lx / self.xn, 3.0) - pow(1.0 - self.ly / self.yn, 3.0))
        self.pp = self.pmax * (1.0 - self.lx / self.xn)
        self.pq = self.pmax * (1.0 - self.ly / self.yn)
        self.pr = self.pmin = 0.0

    def pentagonal_compression_zone_b_equations(self, variables):
        x, y = variables
        a1 = 4 * self.lx * (0.5 - fabs(self.ex) / self.lx)
        b1 = 1 - pow(1 - self.lx / x, 3) - pow(1 - self.ly / y, 3)
        c1 = 1 - pow(1 - self.lx / x, 4) - pow(1 - self.ly / y, 4) - 4 * pow(1 - self.lx / x, 3) * self.lx / x
        f1 = x - a1 * b1 / c1
        a2 = 4 * self.ly * (0.5 - fabs(self.ey) / self.ly)
        b2 = 1 - pow(1 - self.lx / x, 3) - pow(1 - self.ly / y, 3)
        c2 = 1 - pow(1 - self.lx / x, 4) - pow(1 - self.ly / y, 4) - 4 * pow(1 - self.ly / y, 3) * self.ly / y
        f2 = y - a2 * b2 / c2
        return (f1, f2)

    def full_compression_zone_c(self):
        self.xn = self.lx * (1.0 + 6.0 * (self.kx + self.ky)) / (12.0 * self.kx)
        self.yn = self.ly * (1.0 + 6.0 * (self.kx + self.ky)) / (12.0 * self.ky)
        self.yp = 0.0
        self.po = self.pmax = self.pm * (1.0 + 6.0 * self.kx + 6.0 * self.ky)
        self.pr = self.pmin = self.pm * (1.0 - 6.0 * self.kx - 6.0 * self.ky)
        self.pp = self.pm * (1.0 - 6.0 * self.kx + 6.0 * self.ky)
        self.pq = self.pm * (1 + 6.0 * self.kx - 6.0 * self.ky)

    def trapezoidal_compression_zone_x_direction_d(self):
        x12 = sqrt(1.0 - 12.0 * pow(self.kx, 2.0))
        x4 = 1.0 + 4.0 * pow(self.kx, 2.0)
        c12 = 0.5
        self.xn = self.lx * (1.0 + 6.0 * self.kx + x12) / (12.0 * self.kx)
        self.yn = c12 * self.ly * (c12 - self.ky) * (2.0 + x12) * (1.0 + 2.0 * self.kx - x12) / (self.kx * x4)
        self.yp = c12 * self.ly * (c12 - self.ky) * (2.0 + x12) * (-1.0 + 2.0 * self.kx + x12) / (self.kx * x4)
        self.po = self.pmax = (self.pm / 3.0) * (2.0 - x12) * (1.0 + 6.0 * self.kx + x12) / (c12 - self.ky)
        self.pp = (self.pm / 3.0) * (2.0 - x12) * (1.0 - 6.0 * self.kx + x12) / (c12 - self.ky)
        self.pr = self.pq = self.pmin = 0.0

    def trapezoidal_compression_zone_y_direction_e(self):
        y12 = sqrt(1.0 - 12.0 * pow(self.ky, 2.0))
        y4 = 1.0 + 4.0 * pow(self.ky, 2.0)
        c12 = 0.5
        self.xn = c12 * self.lx * (c12 - self.kx) * (2.0 + y12) * (1.0 + 2.0 * self.ky - y12) / (self.ky * y4)
        self.yn = self.ly * (1.0 + 6.0 * self.ky + y12) / (12.0 * self.ky)
        self.xq = c12 * self.lx * (c12 - self.kx) * (2.0 + y12) * (-1.0 + 2.0 * self.ky + y12) / (self.ky * y4)
        self.po = self.pmax = self.pm * (2.0 - y12) * (1.0 + 6.0 * self.ky + y12) / (c12 - self.kx) / 3.0
        self.pq = self.pm * (2.0 - y12) * (1.0 - 6.0 * self.ky + y12) / (c12 - self.kx) / 3.0
        self.pp = self.pr = self.pmin = 0.0

    def corner_pressures(self):
        if self.ex >= 0.0 and self.ey >= 0.0:
            return self.po, self.pp, self.pr, self.pq
        elif self.ex < 0.0 and self.ey > 0.0:
            return self.pp, self.po, self.pq, self.pr
        elif self.ex <= 0.0 and self.ey < 0.0:
            return self.pr, self.pq, self.po, self.pp
        elif self.ex > 0.0 and self.ey < 0.0:
            return self.pq, self.pr, self.pp, self.po
        else:
            return 0.0, 0.0, 0.0, 0.0

    def arrange_pressure_point(self, x, y):
        if self.p3 == self.pmax:
            x = self.lx - x
            y = self.ly - y
        elif self.p2 == self.pmax:
            x = self.lx - x
        elif self.p4 == self.pmax:
            y = self.ly - y
        return x, y

    def arrange_pressure_point_by_centroid_cs(self, x, y):
        if self.p3 == self.pmax:
            x = - x
            y = - y
        elif self.p2 == self.pmax:
            x = - x
        elif self.p4 == self.pmax:
            y = - y
        return x, y

    def pressure_at_point(self, x, y):
        x, y = self.arrange_pressure_point(x, y)
        return self.pmax * (-x / self.xn - y / self.yn + 1)

    def pressure_at_point_by_centroid_cs(self, x, y):
        x, y = self.arrange_pressure_point_by_centroid_cs(x, y)
        return self.pmax * (-x / self.xn - y / self.yn + 1 - 0.5 * (self.lx / self.xn + self.ly / self.yn))

1, 2, 3 ve 4 köşe gerilmelerini hesaplarken dikkate alınan pozitif yönler ve buna bağlı eksantristeler Şekil-2’de verilmiştir.

Şekil-2

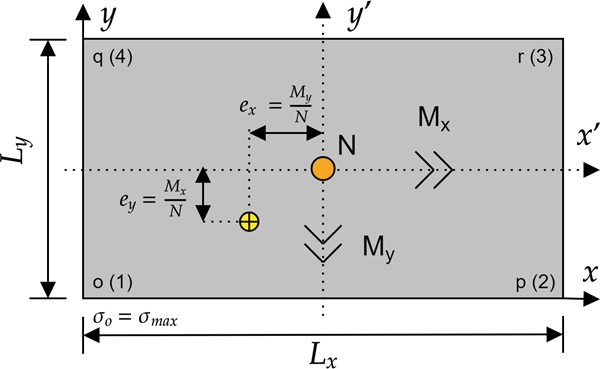
RectFootingPressDistribution sınıfının kullandığı parametreler ve hesapladığı değerler ise aşağıdaki gibidir.

$L_x:$ x yönündeki temel genişliği (m)

$Ly:$ y yönündeki temel genişliği (m)

$M_x:$ x-x ekseni etrafında moment (t.m)

$M_y:$ y-y ekseni etrafında moment (t.m)

$N:$ Eksenel kuvvet (t)

$\sigma_{o}, \sigma_{p}, \sigma_{r}, \sigma_{q}:$ Pozitif $M_x$ ve $M_y$ momentleri için zemin gerilmeleri (t/m²)

$\sigma_{1}, \sigma_{2}, \sigma_{3}, \sigma_{4}:$ Eksantiriste işaretlerine göre düzenlenmiş zemingerilmeleri (t/m²)

$x_n:$ x yönünde gerilmenin sıfır olduğu noktanın gerilmenin maksimum olduğu köşeye (o) uzaklığı(m)

$y_n:$ y yönünde gerilmenin sıfır olduğu noktanın gerilmenin maksimum olduğu köşeye (o) uzaklığı (m)

$x_q:$ x yönünde gerilmenin sıfır olduğu noktanın (q) köşesine uzaklığı (m)

$y_p:$ y yönünde gerilmenin sıfır olduğu noktanın (p) köşesine mesafesi (m)

1. Bellos, John & Bakas, Nikolaos. (2017). Complete Analytical Solution for Linear Soil Pressure Distribution under Rigid Rectangular Spread Footings. International Journal of Geomechanics. ↩

2. Özmen, G. (2011). “Determination of base stresses in rectangular footings under biaxial bending.” Teknik Dergi, 22, 5659-5674. ↩